4.4 The Shape of a Graph
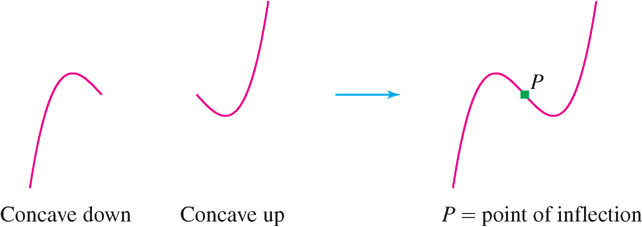
In the previous section, we studied the increasing/decreasing behavior of a function, as determined by the sign of the derivative. Another important property is concavity, which refers to the way the graph bends. Informally, a curve is concave up if it bends up and concave down if it bends down (Figure 4.35).
To analyze concavity in a precise fashion, let’s examine how concavity is related to tangent lines and derivatives. Observe in Figure 4.36 that when \(f(x)\) is concave up, \(f'(x)\) is increasing (the slopes of the tangent lines increase as we move to the right). Similarly, when \(f(x)\) is concave down, \(f'(x)\) is decreasing. This suggests the following definition.
DEFINITION Concavity
Let \(f(x)\) be a differentiable function on an open interval \((a, b)\). Then
- \(f\) is concave up on \((a, b)\) if \(f'(x)\) is increasing on \((a, b)\).
- \(f\) is concave down on \((a, b)\) if \(f'(x)\) is decreasing on \((a, b)\).
EXAMPLE 1 Concavity and Stock Prices
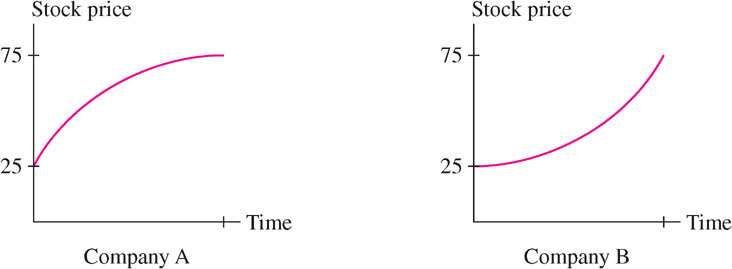
The stocks of two companies, A and B, went up in value, and both currently sell for $75 (Figure 4.37). However, one is clearly a better investment than the other. Explain in terms of concavity.
235
Solution The graph of Stock A is concave down, so its growth rate (first derivative) is declining as time goes on. The graph of Stock B is concave up, so its growth rate is increasing. If these trends continue, Stock B is the better investment.
GRAPHICAL INSIGHT
Keep in mind that a function can decrease while its derivative increases. In Figure 4.38, the derivative \(f'(x)\) is increasing. Although the tangent lines are getting less steep, their slopes are becoming less negative.
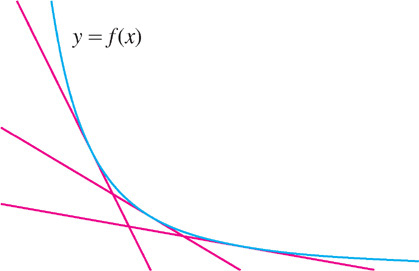
The concavity of a function is determined by the sign of its second derivative. Indeed, if \(f''(x) > 0\), then \(f'(x)\) is increasing and hence \(f(x)\) is concave up. Similarly, if \(f''(x) < 0\), then \(f'(x)\) is decreasing and \(f(x)\) is concave down.
THEOREM 1 Test for Concavity
Assume that \(f''(x)\) exists for all \(x \in (a, b)\).
- If \(f''(x) > 0\) for all \(x \in (a, b)\), then \(f\) is concave up on \((a, b)\).
- If \(f''(x) < 0\) for all \(x \in (a, b)\), then \(f\) is concave down on \((a, b)\).
Of special interest are the points on the graph where the concavity changes. We say that \(P = (c, f(c))\) is a point of inflection of \(f(x)\) if the concavity changes from up to down or from down to up at \(x = c\). Figure 4.39 shows a curve made up of two arcs—one is concave down and one is concave up (the word “arc” refers to a piece of a curve). The point \(P\) where the arcs are joined is a point of inflection. We will denote points of inflection in graphs by a solid square.
According to Theorem 1, the concavity of \(f\) is determined by the sign of \(f''\). Therefore, a point of inflection is a point where \(f''(x)\) changes sign.
THEOREM 2 Test for Inflection Points
Assume that \(f''(x)\) exists. If \(f''(c) = 0\) and \(f''(x)\) changes sign at \(x = c\), then \(f(x)\) has a point of inflection at \(x = c\).
EXAMPLE 2
Find the points of inflection of \(f(x) = \cos x\) on \([0, 2\pi ]\).
Solution We have \(f''(x) = -\cos x\), and \(f''(x) = 0\) for \(x=\frac{\pi}{2},\frac{3\pi}{2}\). Figure 4.40 shows that \(f''(x)\) changes sign at \(x=\frac{\pi}{2}\) and \(x=\frac{3\pi}{2}\), so \(f(x)\) has a point of inflection at both points.
Question 4.11 Concavity Progress Check 1
5VToBYgHxr623KghQ3ONvbKkiopccDNbYCA9xNk4jTqLST1dob4tfzv5ypOKkP407/nxzmsEVs+XMlwZP+QwycQzYq2zut8Xb8Bl/UnOZ/Otwld+EXAMPLE 3 Points of Inflection and Intervals of Concavity
Find the points of inflection and intervals of concavity of \(f(x) = 3x^{5} - 5x^{4} + 1\).
Solution The first derivative is \(f'(x) = 15x^{4} - 20x^{3}\) and
\[f''(x) = 60x^{3} - 60x^{2} = 60x^{2}(x - 1)\]
236
The zeroes of \(f''(x) = 60x^{2}(x - 1)\) are \(x = 0, 1\). They divide the \(x\)-axis into three intervals: \((-\infty , 0)\), \((0, 1)\), and \((1, \infty )\). We determine the sign of \(f''(x)\) and the concavity of \(f\) by computing “test values” within each interval (Figure 4.41):
| Interval | Test Value | Sign of \(f''(x)\) | Behavior of \(f(x)\) |
|---|---|---|---|
| \((-\infty , 0)\) | \(f''(-1) =-120\) | \(-\) | Concave down |
| \((0, 1)\) | \(f''\left(\frac{1}{2}\right)=-\frac{15}{2}\) | \(-\) | Concave down |
| \((1, \infty )\) | \(f''(2) = 240\) | \(+\) | Concave up |
We can read off the points of inflection from this table:
- \(c = 0\): no point of inflection, because \(f''(x)\) does not change sign at 0.
- \(c = 1\): point of inflection, because \(f''(x)\) changes sign at 1.
Question 4.12 Concavity Progress Check 2
yzy6xmnHhC08cV8DfJZAeaQbafDkdD8cHDCfQU4ptuIuG6EWBFfzm6GyqamqqfkThN5xg+uvkynY+Su6C1l21pnPod6I2NgcR3oDI1T8j3Y7pJAJv40hkWrI0r6TUjZXKCm5Sm8fQY+C1nLUmKs1xEIsc1DH++//aM3jz+6F4JhQU72sk6mlI2n4cnTx9vZmMFxF+l3L0Iz6qRy4SkoBj9+zrrW1ilhDffk56+5AqjV4Pi/tvXhHxjcOhS8icvVdJrvlEsEaRPtvRHEFZPTcPNR8CUVLkCSNe/neyTunPAC56I4dDjKqmNlruBXrQ4IekUqkFHYMxqpuwAmVl9fqNGXM4Wj6eEBDMvPvP8BYWLPXnRcYX9SuoJnaIjRux8C7UGlDZnATJR2G7FSsL7BE0+XtvYqfZ+qiV0F+H0B6dmVCL/EDPCUx+o2UTkMmULb4M98q4HBdGjvxSdHBmekZtg0SqCyCHIrUKnJl3BII/c0xT89fwnqvHMixMSD51muKnW2smHjQ1d/QO2QIUF5o03vHiLu+mqtPmj3gWbRl+8U=Usually, we find the inflection points by solving \(f''(x) = 0\). However, an inflection point can also occur at a point \(c\) where \(f''(c)\) does not exist.
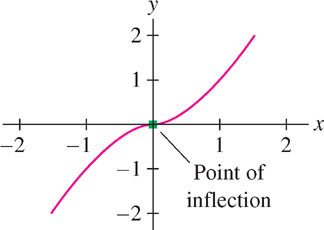
EXAMPLE 4 A Case Where the Second Derivative Does Not Exist
Find the points of inflection of \(f(x) = x^{\frac{5}{3}}\).
Solution In this case, \(f'(x)=\frac{5}{3}x^{\frac{2}{3}}\) and \(f''(x) = \frac{10}{9}x^{-\frac{1}{3}}\). Although \(f''(0)\) does not exist, \(f''(x)\) does change sign at \(x = 0\):
\[ f''(x) = \frac{10}{9x^{1/3}} = \begin{cases}>0&\text{for }x>0\\<0&\text{for }x<0\end{cases} \]
Therefore, the concavity of \(f(x)\) changes at \(x = 0\), and \((0, 0)\) is a point of inflection (Figure 4.42).
Question 4.13 Concavity Progress Check 3
The function \(\displaystyle f(x) = x^4-16\) GnKt4TYsNxa4Dp857L0T1UBnY2J6U0T0 an inflection point at \(c=0\) since CFYfM1BeUKmPyk8E8cPn5TAUWUH9YLZ94C40cluDb9taPsrSEpNI7BbDEDL3PWrLc8dZc7KErWIS9jIo.
The function \(\displaystyle f(x) = |x|e^x\) eULJo1suB4Zdw9jnksmPb25iQpdujKLJ an inflection point at \(c=0\) since cwIDy5XSudJdEAOGSRbg0OCZB0cAJvB4dA2wg2UwQoSDbqn/H4cVHk3M0+rgmaCe3YkwxsIWlurCNRE7TZ1Bk2oFah+QeazC+XgSn8dusqQ+VX21.
GRAPHICAL INSIGHT
Points of inflection are easy to spot on the graph of the first derivative \(f'(x)\). If \(f''(c) = 0\) and \(f''(x)\) changes sign at \(x = c\), then the increasing/decreasing behavior of \(f'(x)\) changes at \(x = c\). Thus, inflection points of f occur where \(f'(x) \) has a local min or max (Figure 4.43).
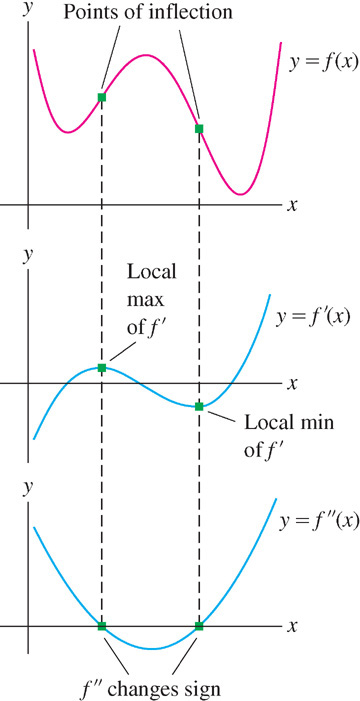
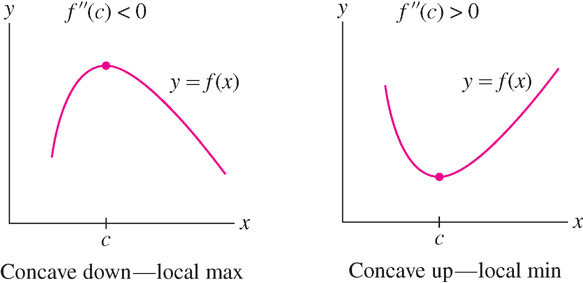
4.4.1 Second Derivative Test for Critical Points
There is a simple test for critical points based on concavity. Suppose that \(f'(c) = 0\). As we see in Figure 4.45, \(f(c)\) is a local max if \(f(x)\) is concave down, and it is a local min if \(f(x)\) is concave up. Concavity is determined by the sign of \(f''\), so we obtain the following Second Derivative Test. (See Exercise 63 for a detailed proof.)
237
THEOREM 3 Second Derivative Test
Let \(c\) be a critical point of \(f(x)\). If \(f''(c)\) exists, then
- \(f''(c)>0\implies f(c)\text{ is a local minimum.}\)
- \(f''(c)<0\implies f(c)\text{ is a local maximum.}\)
- \(f''(c)=0\implies \text{inconclusive: }f(c)\text{ may be a local min, a local max, or neither.}\)
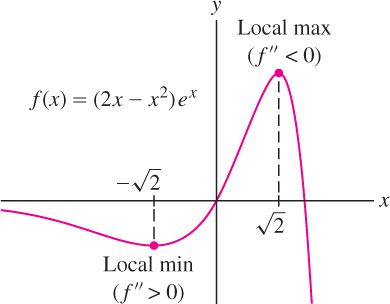
EXAMPLE 5
Analyze the critical points of \(f(x) = (2x - x^{2})e^{x}\).
Solution First, solve
\[ f'(x) = (2x - x^{2})e^{x} + e^{x}(2 - 2x) = (2 - x^{2})e^{x} = 0 \]
The critical points are \(c=\pm\sqrt{2}\) (Figure 4.46). Next, determine the sign of the second derivative at the critical points:
\begin{eqnarray*} f''(x) = (2-x^2)e^x + e^x(-2x)&=&(2-2x-x^2)e^x\\ f''(-\sqrt{2})=(2-2(-\sqrt{2})-(-\sqrt{2})^2)e^{-\sqrt{2}}&=&2\sqrt{2}e^{-\sqrt{2}}&>0&\text{(local min)}\\ f''(\sqrt{2})=(2-2(\sqrt{2})-(\sqrt{2})^2)e^{\sqrt{2}}&=&-2\sqrt{2}e^{\sqrt{2}}&<0&\text{(local max)}\\ \end{eqnarray*}
By the Second Derivative Test, \(f(x)\) has a local min at \(c=-\sqrt{2}\) and a local max at \(c=\sqrt2\) (Figure 4.46).
Question 4.14 Second Derivative Test Progress Check 1
The function \(\displaystyle f(x)= -2x^3+3x^2+36x\) has two critical points, \(c_1\) and \(c_2\). Find them and use the second derivative test to classify them.
\(f(x) \) has a local CoKdRWMwar7l2TXZp/HL1V0+ugY= at the smaller critical point \(c_1=\)FmAhxBkQqN0= since /walsKZynu95yaV2kfrdxTcgJ48Vu3+jjoxjX97nXaoJMqwHAdmTUQ==.
\(f(x) \) has a local MLrjsAZLmRw2xfA/t8djnqWlqT8= at the larger critical point \(c_2=\)607M7xmPORU= since jYsZB+VLxFNf//k2OwtTVlGcUTkT0+OituVrLLHd+KUIUjZoVXhC0Q==.
EXAMPLE 6 Second Derivative Test Inconclusive
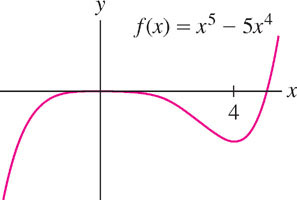
Analyze the critical points of \(f(x) = x^{5} - 5x^{4}\).
Solution The first two derivatives are
\begin{align*} f'(x)&=5x^4 - 20x^3 = 5x^3(x-4)\\ f''(x)&=20x^3 - 60x^2 \end{align*}
The critical points are \(c = 0, 4\), and the Second Derivative Test yields
\begin{eqnarray*} f''(0)&=&0&\implies&\text{Second Derivative Test fails.}\\ f''(4)&=&320>0&\implies&f(4)\text{ is a local min.} \end{eqnarray*}
The Second Derivative Test fails at \(c = 0\), so we fall back on the First Derivative Test. Choosing test points to the left and right of \(c = 0\), we find
\begin{eqnarray*} f'(-1)&=&5+20=25>0&\implies&f'(x)\text{ is positive on }(-\infty,0)\\ f'(1)&=&5-20=-15<0&\implies&f'(x)\text{ is negative on }(0,4) \end{eqnarray*}
Since \(f'(x)\) changes from \(+\) to \(-\) at \(c = 0\), \(f(0)\) is a local max (Figure 4.47).
Question 4.15 Second Derivative Test Progress Check 2
H/QQ13KrZxM4jUKVG7xUYb5unSV0mILOlCM0EAeVN3PrdjgxXbksZy6FzsNowiQdTMjtNVwr/0loX9/pz3ILul8KC60+YkzKSFrQacax46vnRXndUw+fw4pJ/lYo0e9rew3QrguG+8oZmLA6pJhxzq6Kf8gTEUlqSJaWnLY9nVnJF/dwXhemE+tkDiz1flfhZRTzGo3FLWfsF7g7f7w5rzt3upjRoUZ0lUgi8hma1P2wR23tJZFbTXp5kzBkRG1zP4PEpgkwotbYCM7GFp6C9zlTA85zgHm9PJKZgT/hxrnbsC6FSVxc6DQJyG21aVhKnmhjFoOJlMmiDBcljgNYo0HFaKXhuFzt82+zoUO9wvRSuWgdlE1otYNSQdRFBTGl+xo6kF4mQud0WEetLUZ04HHz5FzJlhFQXCncjGsmcXxJQiADXLr55Sb++jh4Ff6tCAAcaTz7FVSlsnhrjuHeW/TTthrQa1BSI5BOCpsjJAkLv/lxdZi4e0s5TOU3NGoWx7T0RnPmjhulYWJ5BIjey7dzFqXOYiT7OG1+Vzj1pRIJmgStXdQzWOi73zPpPzn0XkzTIMk/zwPZx28ZMwx6NAls5JYOM/dxjOLwbQdOfVBs7jTYhlH1eqGJgdUwX7v34YsVw6iHf1dSik4PN2GdJPY+9pIyzHBfrV6H6/Dgyh7oi/nUkpsCIfdHfup2gts+dIK6ihcUFPnIOgUcjDUZvXUnFU7spsvTfV4c5OAg7LHWnWM2d+IFfhf4jzzL+ZGECvjy2ngVAQ+3oBuLV8pHK+BiRSlyQm8hoIInR6pU1omNqjO04AkYpO2we2JNQ3CnvIr2Y2dZJ6M3lGLVn4d+gmI3wtpswSn2k9Mpnei1GXrsfS7yk4AXnLSQUF34cNx5/FCcHbB1PxwSESKfV/DC8J7FFUrbGVpcmbnxmeUCen+ZMDIxQe9DMSiww4hv+/zbf2Pcpg3Bp3BlwGuhPT7FjmM+0qMpf4aXdohdGg53hsZp1x0pbZT3skbu9lA/ogmdtVEVe1zAM8+SW38Z4.4.2 Section 4.4 Summary
- A differentiable function \(f(x)\) is concave up on \((a, b)\) if \(f'(x)\) is increasing and concave down if \(f'(x)\) is decreasing on \((a, b)\).
238
- The signs of the first two derivatives provide the following information:
| First Derivative | Second Derivative |
|---|---|
| \(f' > 0 \implies f\text{ is increasing}\) | \(f'' > 0 \implies f\text{ is concave up}\) |
| \(f' < 0 \implies f\text{ is decreasing}\) | \(f'' < 0 \implies f\text{ is concave down}\) |
- A point of inflection is a point where the concavity changes from concave up to concave down, or vice versa.
- If \(f''(c) = 0\) and \(f''(x\)) changes sign at \(c\), then \(c\) is a point of inflection.
- Second Derivative Test: If \(f'(c) = 0\) and \(f''(c)\) exists, then
–\(f(c)\) is a local maximum if \(f''(c) < 0\).
–\(f(c)\) is a local minimum if \(f''(c) > 0\).
– The test fails if \(f''(c) = 0\).
If the test fails, use the First Derivative Test.